#简介
并查集算法,也叫Union-Find算法,主要用于解决图论中的动态连通性问题。
#算法类
这里直接给出并查集算法类UnionFind.class,如下:
/**
* Union-Find 并查集算法
* @author Chiaki
*/
public class UnionFind {
// 连通分量个数
private int count;
// 存储若干棵树
private int[] parent;
// 记录树的"重量"
private int[] size;
// 构造函数
public UnionFind(int count) {
this.count = count;
parent = new int[count];
size = new int[count];
for (int i = 0; i < count; i++) {
parent[i] = i;
size[i] = 1;
}
}
// 连通函数
public void union(int p, int q) {
// 如果节点p和q已经连接,直接返回
if (connected(p,q)) return;
// 找到节点p和节点q的根节点
int rootP = find(p);
int rootQ = find(q);
if (size[rootP] > size[rootQ]) {
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
} else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
count--;
}
// 判断是否连通
public boolean connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
// 寻找根节点
public int find(int x) {
while (parent[x] != x) {
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
// 返回连通分量个数
public int count() {
return count;
}
}
下面逐步解释Union-Find算法类中的变量定义以及相关函数。
#成员变量
可以看到该类中定义了三个成员变量,分别是int count、int[] parent以及int[] size。
int count:可以理解为连通分量的个数。
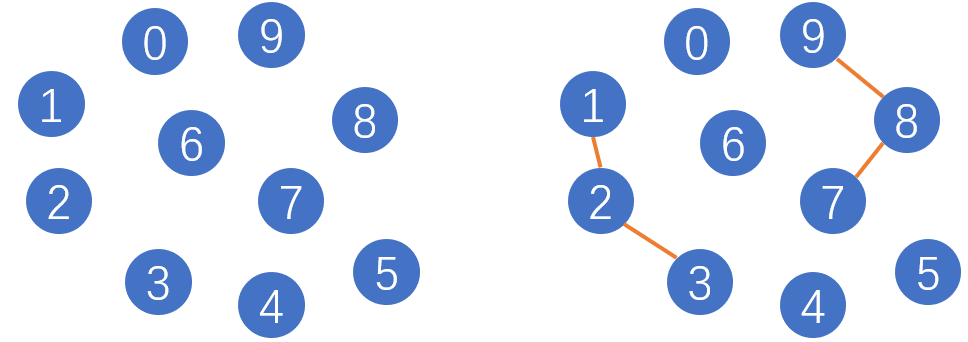
如上左图所示,共有10个节点(分量),此时连通分量的个数为10。如上右图所示,在进行连通操作(union)后,分量之间存在了连接关系(connected),因此此时的连通分量个数为6。
int[] parent:定义父节点数组。说到父节点数组,这里使用多棵树来表示连通性。规定树中的每个节点都有一个指针指向其父节点。一开始没有连通,此时每个节点指向父节点的指针都是指向自己,也就是根节点;当两个节点被连通,就让其中的任意一个节点的根节点接到另一个节点的根节点上,如下图所示。
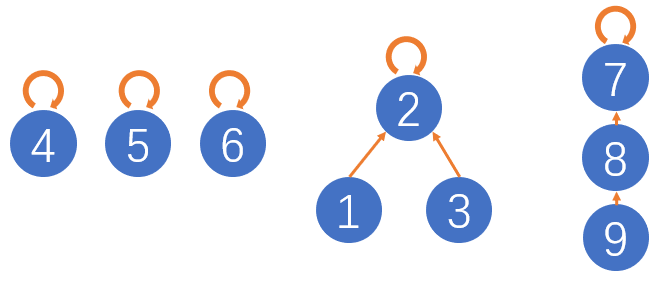
此时,可以得到:若节点p和节点q连通,那么它们一定有相同的根节点。
int[] size:记录每一棵树中节点的数量,称之为树的重量,以此方便对树的平衡性进行优化。如上张图所示,如果要把节点3和节点7连接(union),此时树的情况如下图所示:
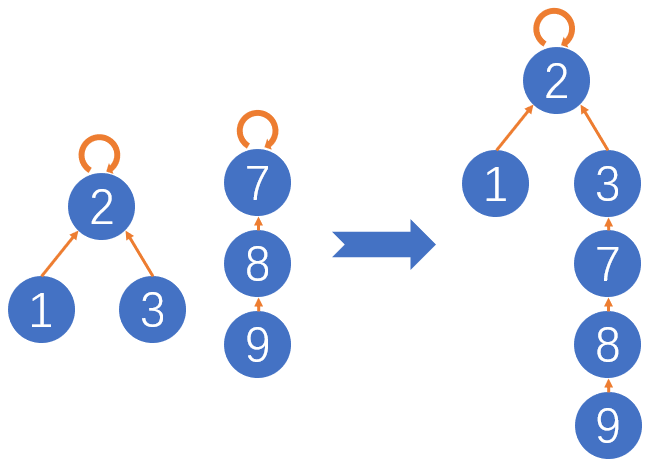
此时,可以看出,树的平衡性出现了问题,因此我们需要借助树的重量,即int[] size数组对节点的连接操作(union)进行平衡性优化。
#构造函数
UnionFind类构造函数的参数为int n,即初始的节点数目,亦即初始连通分量的个数。在进行初始化操作时,主要是初始化父节点数组int[] parent以及每棵树中节点的数目数组int[] size。在初始情况下,每个节点的父节点都是自身,而每棵树中节点的个数都是1,因此构造函数如下:
public UnionFind(int count) {
this.count = count;
parent = new int[count];
size = new int[count];
for (int i = 0; i < count; i++) {
parent[i] = i;
size[i] = 1;
}
}
#其他函数
在上面的介绍中,我们知道,在UnionFind类中最重要的操作就是连接(union)操作。然而,在将节点p和节点q连接时,需要把一个节点(假定为节点p)的指针指向另一个节点(假定为节点q)的父节点,因此,我们需要先实现一个int find(int x)函数来找到一个节点的父节点,如下所示:
public int find(int x) {
while (parent[x] != x) {
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
另外,实现boolean connected(int p, int q)函数判断节点p和节点q是否处于连接状态,如下:
public boolean connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
在实现int find(int x)函数和boolean connected(int p, int q)函数后,接下来要实现最关键的连接操作,即void union(int p, int q)函数,如下所示:
public void union(int p, int q) {
// 如果节点p和q已经连接,直接返回
if (connected(p,q)) return;
// 找到节点p和节点q的根节点
int rootP = find(p);
int rootQ = find(q);
// 根据size数组进行平衡化操作:小树接到大树下
if (size[rootP] > size[rootQ]) {
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
} else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
// 连接完成后,连通分量减一
count--;
}
最后,完成连通分量计数函数int count(),如下:
public int count() {
return count;
}
#应用
在介绍完并查集算法类UnionFind.class后,下面来看看该算法的应用。
#朋友圈/好友关系问题
这个问题是并查集的一个典型应用,印象中猿辅导的算法手撕中这个题出现的频率比较高。问题描述如下:
班上有 N 名学生。其中有些人是朋友,有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友,B 是 C 的朋友,那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈,是指所有朋友的集合。
给定一个
N * N的矩阵 M,表示班级中学生之间的朋友关系。如果M[i][j]= 1,表示已知第 i 个和 j 个学生互为朋友关系,否则为不知道。你必须输出所有学生中的已知的朋友圈总数。输入输出示例如下:输入:
[[1,1,0], [1,1,0], [0,0,1]]
输出:2
利用并查集来解决该问题(假设UnionFind.class已定义,下同),如下:
class Solution {
public int findCircleNum(int[][] M) {
int n = M.length;
UnionFind uf = new UnionFind(n);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (M[i][j] == 1) {
uf.union(i, j);
}
}
}
return uf.count();
}
}
#岛屿数量
岛屿数量问题其实也是互联网大厂常问的题目之一,除了采用DFS来实现,并查集也可以用于解决这类问题。问题描述如下:
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。此外,你可以假设该网格的四条边均被水包围。输入输出示例如下:
输入:grid = [ ["1","1","1","1","0"], ["1","1","0","1","0"], ["1","1","0","0","0"], ["0","0","0","0","0"] ]
输出:1
采用并查集方法解决:
class Solution {
public int numIslands(char[][] grid) {
int r = grid.length;
if (r == 0) {
return 0;
}
int c = grid[0].length;
int size = r * c;
// 方向数组(向下和向右的坐标偏移)
int[][] directions = {{1, 0}, {0, 1}};
// +1表示虚拟水域,认为网格四条边被水包围
UnionFind uf = new UnionFind(size + 1);
for (int i = 0; i < r; i++) {
for (int j = 0; j < c; j++) {
if (grid[i][j] == '1') {
for (int[] direction : directions) {
int newX = i + direction[0];
int newY = j + direction[1];
if (newX < r && newY < c && grid[newX][newY] == '1') {
uf.union(c * i + j, c * newX + newY);
}
}
} else {
// 如果不是陆地,则所有水域与虚拟水域连接
uf.union(c * i + j, size);
}
}
}
// 减去虚拟水域
return uf.count() - 1;
}
}
#等式方程的可满足性
题目描述如下:
给定一个由表示变量之间关系的字符串方程组成的数组,每个字符串方程
equations[i]的长度为 4,并采用两种不同形式之一:a==b或a!=b。在这里,a 和 b 是小写字母(不一定不同),表示单字母变量名。只有当可以将整数分配给变量名,以便满足所有给定的方程时才返回
true,否则返回false。 输入输出示例如下:输入:["a == b", "b == c", "a == c"] 输出:true
输入:["a == b", "b != c", "c == a"] 输出:false
采用并查集算法解决该问题,如下:
class Solution {
public boolean equationsPossible(String[] equations) {
// 可能出现的26个字母
UnionFind uf = new UnionFind(26);
// 将相等的字母进行连接
for (String e : equations) {
if (e.charAt(1) == '=') {
char x = e.charAt(0);
char y = e.charAt(3);
uf.union(x - 'a', y - 'a');
}
}
// 若已经成立的相等关系被打破就返回false
for (String e : equations) {
if (e.charAt(1) == '!') {
char x = e.charAt(0);
char y = e.charAt(3);
if (uf.connected(x - 'a', y - 'a')) {
return false;
}
}
}
return true;
}
}
#总结
并查集算法主要是解决图中的动态连通性问题。对于类似岛屿数量的问题,注意在初始化并查集时做到+1来表示一个虚拟节点,同时对于其中的二维数组可以采用方向数组int[][] directions = {{1, 0}, {0, 1}}来规范和简化代码。对于等式方程的可满足性,主要是利用了并查集算法的等价特点。